
Quantum-optical metrology, imaging, and sensing
In quantum-optical metrology and quantum imaging, quantum effects of light, and in particular quantum entanglement, are exploited to improve the sensitivity in phase measurements or the spatial resolution of optical systems.
In quantum-optical metrology and quantum imaging, quantum effects of light, and in particular quantum entanglement, are exploited to improve the sensitivity in phase measurements or the spatial resolution of optical systems. In quantum-optical metrology, interferometers are used to measure the optical phase (and in this way e.g., length differences as in gravitational-wave detectors). The common setup is the Mach-Zehnder interferometer (MZI) used with classical coherent light on one input port and the phase is derived from the intensity difference at the output ports. The sensitivity of the phase measurement then is limited by shot noise to the standard quantum limit (n is the number of photons and proportional to the light intensity). One can show that the absolute limit given by quantum theory is the considerably lower Heisenberg limit . There are two known ways to beat the standard quantum limit. In the common setup, no light (i.e. the quantum vacuum) enters the second input port of the MZI, and this is the main reason for the large phase noise. If instead, squeezed light is put into the second input port, the phase noise can be reduced considerably. However, strongly squeezed light is difficult to produce. An alternative is to use entangled states of light, and in particular the so-called NOON state. This state is a superposition of having photons in the first and photons in the second MZI arm and having photons in the first and photons in the second MZI arm. Passing through a phase shifter , classical coherent light picks up a phase difference of while the NOON state picks up the -fold larger phase difference of . This brings the phase noise down to the Heisenberg limit and is called super-sensitivity. However, there are severe challenges. First, it is difficult to prepare NOON states. In the easiest case , usually parametric down conversion is used to generate photon pairs and this process is very inefficient. Another challenge is the measurement: the photon detectors need to be able to distinguish photon numbers at the level of single photons.
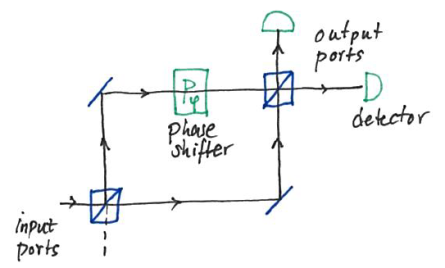
In quantum imaging, quantum effects of light are used to improve optical imaging. NOON states, for instance, can be used to beat the Rayleigh diffraction limit for the resolution of an imaging system, which is pursued in quantum lithography („super-resolution“). A completely different technique is ghost imaging.
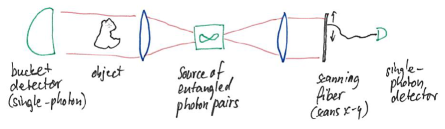
Here, the object and the detector used for imaging are illuminated by two spatially separated, albeit correlated light beams, and the image is obtained by measuring intensity correlations. In the first demonstration of this effect, entangled photon pairs have been used. One of the photons was used to illuminate the object and it was detected with a bucket detector (single-photon detector without spatial resolution) and the other photon was detected far from the object with a scanning single-photon detector. Coincidence counts then produced the image of the object.



